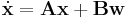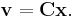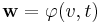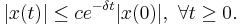Circle criterion
In nonlinear control, the circle criterion is an important theorem in showing the stability of nonlinear time-varying systems. It can be viewed as a generalization of the Nyquist stability criterion for LTI systems.
Overview
Consider a linear system subject to non-linear feedback, i.e. a non linear element 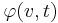 is present in the feedback loop. Assume that the element satisfies a sector condition
is present in the feedback loop. Assume that the element satisfies a sector condition ![[\mu_1,\mu_2]](/2012-wikipedia_en_all_nopic_01_2012/I/0899a13aec82f163c10969a04f3c022d.png) , and (to keep things simple) that the open loop system is stable. Then the closed loop system is globally asymptotically stable if the Nyquist locus does not penetrate the circle having as diameter the segment
, and (to keep things simple) that the open loop system is stable. Then the closed loop system is globally asymptotically stable if the Nyquist locus does not penetrate the circle having as diameter the segment ![[-1/\mu_1,-1/\mu_2]](/2012-wikipedia_en_all_nopic_01_2012/I/57d6425550b5798e3a9bc5023d7f2fae.png) located on the x axis.
located on the x axis.
General description
Consider the nonlinear system
Suppose that
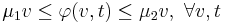
![\det(i\omega I_n-A) \neq 0,\ \forall \omega \in R^{-1}\text{ and }\exists \mu_0 \in [\mu_1, \mu_2]\,:\, A%2B\mu_0 BC](/2012-wikipedia_en_all_nopic_01_2012/I/d0e9304952f380117778298d316b2203.png) is stable
is stable![\Re\left[(\mu_2 C(i\omega I_n-A)^{-1}B-1)(1-\mu_1C(i\omega I_n-A)^{-1}B)\right]<0 \ \forall \omega \in R^{-1}.](/2012-wikipedia_en_all_nopic_01_2012/I/d7a206681aaeeabe31d6e30f761851cc.png)
Then 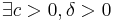 such that for any solution of the system the following relation holds:
such that for any solution of the system the following relation holds:
Condition 3 is also known as the frequency condition. Condition 1 the sector condition.